NPR for local graph partitioning


We developed a new method for local graph partitioning based on a nonlinear generalisation of the PageRank problem involving the Moore-Penrose inverse of the incidence matrix. The Levenberg-Marquardt method is used with a full rank Jacobian variant to obtain a numerical solution to the generalised problem. Sets of vertices are formed according to the ranking supplied by the solution, and a conductance criterion decides upon the set that best represents the local cluster around a starting vertex.
The MATLAB code and the input graphs are available here.
Sparse QUadratic Inverse Covariance matrix estimation (SQUIC)

SQUIC is an $\ell_1$-regularized maximum likelihood method for performant large-scale sparse precision matrix estimation. The code is packaged as the shared library libSQUIC, intended for Linux and Mac OS. It is written in C++ and is parallelized with OpenMP, with Python and R APIs available.
The shared library can be downloaded and used directly, or compiled from source, from this link.
Spectral clustering for source rocks
Oil-oil and oil-source geochemical correlation is a subject of prime importance to the hydrocarbon exploration community for decades. We present a direct multiway spectral clustering approach, which is a graph based method that allows the automatic selection of the optimal number of clusters based on the modularity of the resulting partitioning.
The MATLAB code can be downloaded and used directly from this link.
Multiway p-spectral graph cuts on Grassmann manifolds
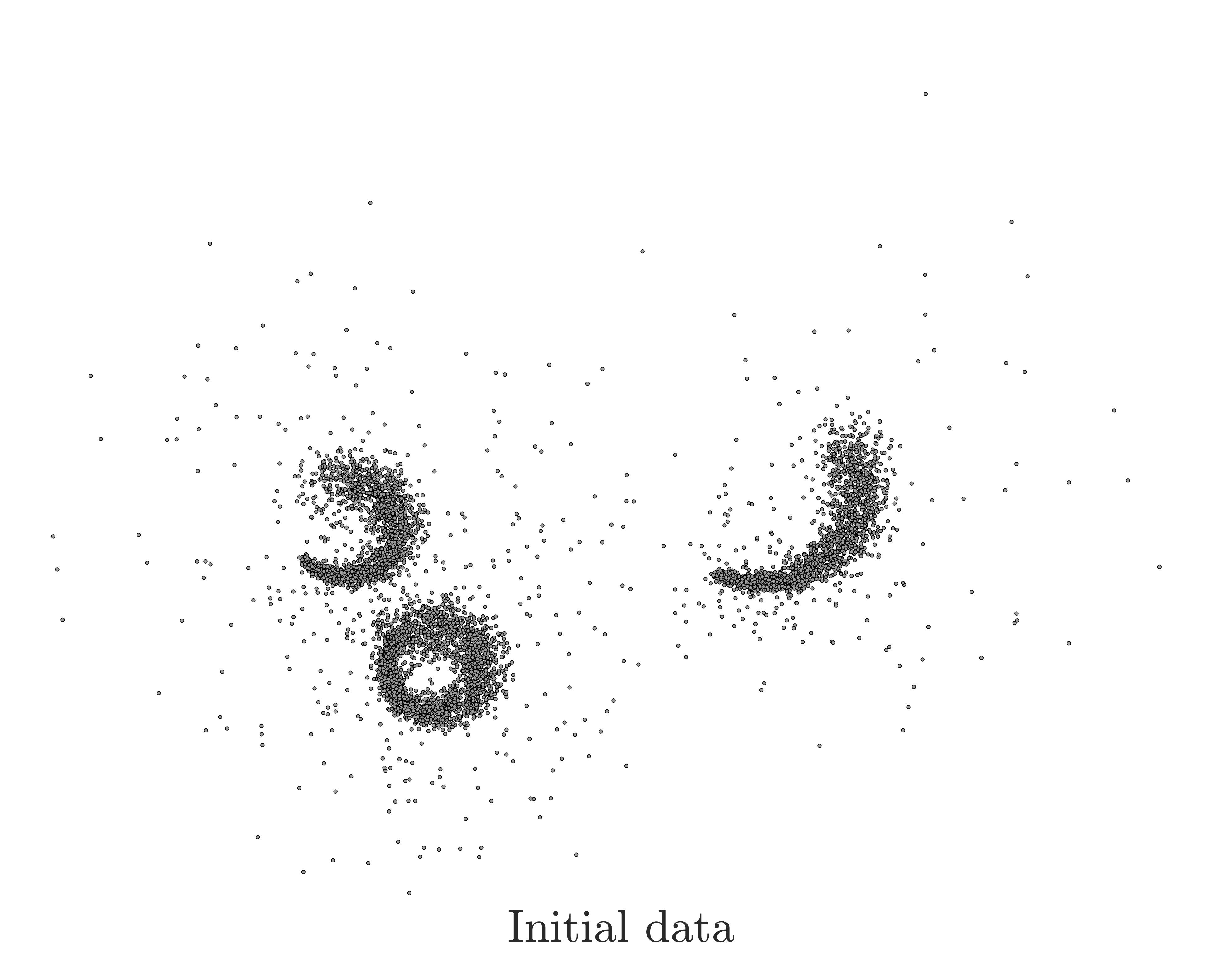

In this work, we developed a new method for multiway p-spectral clustering that leverages recent advancements in Riemannian optimization. This was achieved by reformulating the problem of obtaining multiple eigenvectors of the graph p-Laplacian as an unconstrained minimization problem on a Grassmann manifold.
The MATLAB code with mex executables can be downloaded and used directly from this link.
